モデリング

3.4. モデリング#

TII Spectrometryのモデリングパッケージを使用すると、予測モデルを構築して使用し、スペクトルデータセットを分析できます。スペクトルを入力として使用する、2種類の分析が利用可能です。

  • 回帰分析：回帰は、予測したい出力プロパティが、濃度、品質スコア、温度、水分レベルなどの連続的な数値変数である場合に使用されます。典型的な例としては、化学溶液の吸収スペクトルを使用して溶質の正確な濃度を予測する濃度予測があり、これはしばしばベール・ランバートの法則に依存します。

  • 分類分析：分類は、予測したい出力プロパティが、材料タイプ、欠陥の有無、グレードレベルなどの離散的なカテゴリカルラベルまたはクラスである場合に使用されます。典型的な例としては、材料の識別が挙げられます。IRスペクトルに基づいて、未知のプラスチックサンプルをポリプロピレン（PP）またはポリエチレン（PE）として分類します。

モデリングパッケージは分析 ‣ モデリング ‣ トレーニング/予測を使用してアクセスでき、任意の分光器で利用可能です。

参考

これを実際に確認するには、応用例例プラスチックの識別を参照してください。

3.4.1. 概要#

回帰および分類分析の詳細については、専用のセクションで説明します。

ただし、どちらのタイプの分析にも共通のワークフローがあります。

  1. 既知の材料のスペクトル（分類の場合）や既知の濃度のスペクトル（回帰の場合）など、トレーニングデータセットを記録します。

  2. このデータセットを使用してモデルを構築します（トレーニング）。これには通常以下が含まれます。

    • データセットにラベル（数値またはカテゴリカル）を割り当てます

    • データに前処理を行います（例：以下による）。

      • ベースライン補正：不要なバックグラウンド信号のオフセットを削除します。

      • 正規化：スペクトルをスケーリングして、全体的な光強度または光路長の変化を削除します。

      • 平滑化：高周波ノイズを低減します。

      • 切り抜き：不要なスペクトル領域を削除します。

    • モデルをトレーニングします（例：線形回帰を使用して検量線をフィッティング）。

    • モデルを検証します

  3. 一度モデルがトレーニングされると、未知のサンプルを使用して予測に使用できます。モデルは後で使用するためにディスクに保存することもできます。

Tip

トレーニングされたモデルは、TII Spectrometryで以下の場所で使用できます。

  • モニタービューで、分類モデルと回帰モデルの両方を使用してリアルタイム監視を行う場合。

  • タイムラプス記録中に、スペクトルから数値（回帰モデルを使用）を抽出する場合。

注釈

原則として、複数の分光器からの信号をモデルに組み込むことができます（例：分光器が）。

  • 異なるスペクトル範囲をカバーしている場合

  • 異なる場所で同じプロセスを測定している場合

注釈

モデルは、少なくとも原則的にはデバイス非依存です。つまり、ある分光器のスペクトルデータセットでトレーニングされたモデルを、別のデバイスのデータセットで予測に使用できます。ただし、以下の注意事項が適用されます。

  • スペクトルは、デバイス感度の違いを考慮して適切に正規化する必要があります（これはいずれにしてもベストプラクティスです）。

  • スペクトル範囲は（大まかに）一致し、最も重要なことに、モデルが識別するために必要なスペクトル特徴を含んでいる必要があります。ごく簡単な例として、近赤外データでトレーニングされたモデルは、（当然ながら）可視範囲で動作する分光器を使用する場合には機能しません。適切なオーバーラップがあるスペクトル範囲については、TII Spectrometryは補間とパディングを使用してスペクトルデータを変換し、異なるスペクトル分解能を考慮します。

3.4.2. 前処理#

前処理には、ノイズや散乱効果を除去するためのデータの事前処理が含まれます。前処理オプションは回帰モデルと分類モデルで共有されており、同じ論理が両方の種類の分析に適用されます。

注釈

前処理設定はモデルの一部です。それらはモデルファイルに保存され、予測フェーズ中にスペクトルに適用されます。

TII Spectrometryは以下の前処理設定を提供します（図 3.11）。

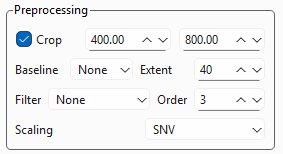
../_images/analysis_modeling_preprocessing.png

図 3.11 前処理設定#

切り抜き

スペクトルのサブ領域を選択できます。

ベースライン

Statistics-sensitive Non-linear Iterative Peak-clipping (SNIP) アルゴリズム (Ryan, 1988)を使用して、データセットから非線形ベースラインを除去します。範囲パラメーターは、ベースラインの曲率を変更します。

注釈

スケーリングを使用して、一定のオフセットを簡単に除去できます。スペクトル取得中のバックグラウンド減算によってベースラインを除去できる場合は、そちらの方が望ましいでしょう。

フィルター

データに畳み込み平滑化フィルターを適用します。設定は、メインウィンドウのフィルター設定と同じです。

スケーリング

データをスケーリング（正規化）します。3つのオプションが利用可能です。

重要

回帰または分類のパフォーマンスにとって、また特に、以下に依存しない汎化されたモデルを達成するために、スケーリングは非常に重要です。

  • 照明条件

  • 分光器の感度または露光時間

TII Spectrometryのスケーリング方法の比較については、表 3.1を参照してください。

3.4.2.1. スケーリング方法#

3.4.2.1.1. 最小-最大スケーリング#

最小-最大スケーリングは、特徴スケーリングまたはユニティベースの正規化とも呼ばれ、数値特徴を特定の事前定義された範囲（通常は\([0, 1]\)）に変換するためのデータ前処理手法です。

単一のスペクトル\(X_i\)の場合、変換は次のようになります。

\[X_{\text{MM}, i} = \frac{X_i - \min(X_i)}{\max(X_i) - \min(X_i)}\]

ここで、

  • \(X_i\)は元のスペクトルです。

  • \(\min(X_i)\)と\(\max(X_i)\)は、その単一のスペクトル内の最小および最大の吸光度/反射率値です。

スペクトルごとの最小-最大スケーリングの主な目的は、光路長、サンプル充填、または光源強度の変化など、スペクトルの大きさに影響を与える要因によって引き起こされる乗法的なスケーリングの違いを除去することです。

  • ベースラインアンカー：この方法では、スペクトル内の最も低いポイントを\(0\)に、最も高いポイントを\(1\)に強制します。これにより、あるサンプルから次のサンプルへの信号強度のダイナミックレンジまたは全体的な広がりの違いが効果的に補正されます。

  • コントラストの保持：スペクトル特徴の相対的な形状と比例性を保持し、ピーク間の高さの比率が一貫していることを保証します。

3.4.2.1.2. 標準正規変量スケーリング#

SNVスケーリングはスペクトルごとの操作であり、データセット内の個々のスペクトル曲線に独立して適用されます。これは、スペクトルをそれ自体の平均と標準偏差に基づいて正規化する2段階のプロセスです。標準正規変量（SNV）スケーリング方法は、分光法、特に近赤外（NIR）データで、ベースライン補正を実行し、スペクトル特徴を標準化するために使用される一般的な手法です。単一のスペクトル\(X_i\)（異なる波長での測定値のベクトル）の場合、スケーリングされたスペクトル\(X_{\text{SNV}, i}\)への変換は次式で与えられます。

\[X_{\text{SNV}, i} = \frac{X_i - \bar{X}_i}{s_i}\]

ここで、

  • \(X_i\)は元のスペクトルです。

  • \(\bar{X}_i\)は、そのスペクトル内のすべての吸光度/反射率値の平均です。

  • \(s_i\)は、そのスペクトル内のすべての吸光度/反射率値の標準偏差です。

この式の結果、平均強度がゼロ付近に集中し、分散（広がり）が1に標準化された新しいスペクトルが得られます。

SNVスケーリングは、サンプルの化学組成に関係のない変動の2つの主要な原因を効果的に除去します。

  1. ベースラインオフセット（加法的効果）：平均（\(\bar{X}_i\)）の減算は、サンプル光路長の変更や、すべての波長で全体的な強度レベルに均等に影響する光散乱変動などの要因によって引き起こされる、スペクトル内の一定の垂直シフトを補正します。

  2. スケーリングの違い（乗法的効果）：標準偏差（\(s_i\)）による除算は、散乱特性、粒子サイズ、または機器の変更の違いによって引き起こされる、スペクトルの傾きまたは全体の大きさの変動を補正します。

これらの物理的な変動を除去することで、SNVは化学組成に真に関連するスペクトル特徴（特徴的な吸収ピーク）を強調し、その後のモデリングをより正確で堅牢なものにします。

表 3.1 最小-最大 vs. SNV#

Feature

Per-Spectrum Min-Max Scaling

Standard Normal Variate (SNV)

Centering Reference

The absolute minimum value of the spectrum.

The mean value (\(\bar{X}_i\)) of the entire spectrum.

Scaling Reference

The range (\(\max - \min\)) of the spectrum.

The standard deviation (\(s_i\)) of the spectrum.

Targeted Error

Primarily Multiplicative scaling (intensity differences).

Both Additive baseline shifts and Multiplicative scaling.

Effect on Peaks

Anchors the lowest point to 0 and stretches/compresses the peaks to fit between 0 and 1.

Centers the whole spectrum around 0, making the negative and positive peak areas equivalent in deviation.

参考

実際的なアプリケーションのコンテキストにおけるデータ前処理の議論については、応用例例プラスチックの識別を参照してください。

3.4.3. 回帰分析#

前述のように、回帰にはスペクトルに数値を割り当てることが含まれます。

TII Spectrometryは、回帰モデルをトレーニングするための2つの異なる方法を提供します（表 3.2）。

  • 線形回帰を使用した手動トレーニング。これには、ピークの面積や2つのピークの強度比など、関連するスペクトル特徴を選択し、それから検量線を構築する必要があります。予測は、この検量線を使用して実行されます。

  • サポートベクター回帰（SVR）に基づく半自動化された機械学習ベースの回帰。二乗誤差の合計を最小限に抑えようとする線形回帰とは対照的に、SVRは、予測されたデータポイントのほとんどがその線から特定の距離内に収まるようにしながら、最適な線または超平面をフィッティングしようとします。非線形関係（スペクトルデータセットでは一般的）の場合、SVRはカーネルトリック（例：動径基底関数またはRBFカーネル）を使用して、入力特徴を高次元空間にマッピングし、元の空間での非線形関係を線形超平面でうまくモデル化できるようにします。この方法は、ノイズや外れ値に対して堅牢であるだけでなく、カーネルを使用してスペクトル特徴と連続的なプロパティ（濃度や品質スコアなど）との間の複雑な非線形関係もモデル化できます。線形回帰とは対照的に、ユーザーによる特徴選択は必要ありません。

表 3.2 線形回帰 vs. SVR#

Feature

Linear Regression

Support Vector Regression (SVR)

Model Type

Parametric (Assumes a linear relationship).

Non-Parametric (Flexible, often uses kernels).

Objective Function

Minimizes the Sum of Squared Errors (SSE), penalizing all errors equally.

Minimizes the errors that fall outside a defined margin (\(\epsilon\)), ignoring small errors within the margin.

Error Treatment

Sensitive to all data points and outliers, especially those far from the line.

Insensitive to data points within the \(\epsilon\)-tube; robust to noise and outliers.

Model Complexity

Simple, easy to interpret, fast to train.

More complex, computationally intensive, especially with kernel methods.

Non-Linearity

Cannot model non-linear relationships without manual feature engineering (e.g., polynomial terms).

Naturally handles non-linear relationships using the Kernel Trick (e.g., RBF kernel).

Key Points

Finds the line that best fits the average of the data.

Finds the line that best fits the boundary defined by the Support Vectors.

Application Suitability

Simple, well-behaved datasets where relationships are known to be linear.

High-dimensional, complex datasets (like spectral data) where non-linear modeling and noise robustness are required.

3.4.3.1. トレーニング#

3.4.3.1.1. 線形回帰#

トレーニングビュー（分析 ‣ モデリング ‣ トレーニング/予測、図 3.12）には、次のユーザーインターフェイス要素が含まれています。

  • 左側のスペクトルサイドバー。トレーニングに使用されるスペクトルとそのラベルが含まれています。

  • スペクトルビュー。前処理後のスペクトルが含まれています。

  • 右側のパラメーターサイドバー。前処理とトレーニングの設定を制御します。

  • 結果ビュー（中央下部）。検量線と、各トレーニングスペクトルの予測数値が含まれています。

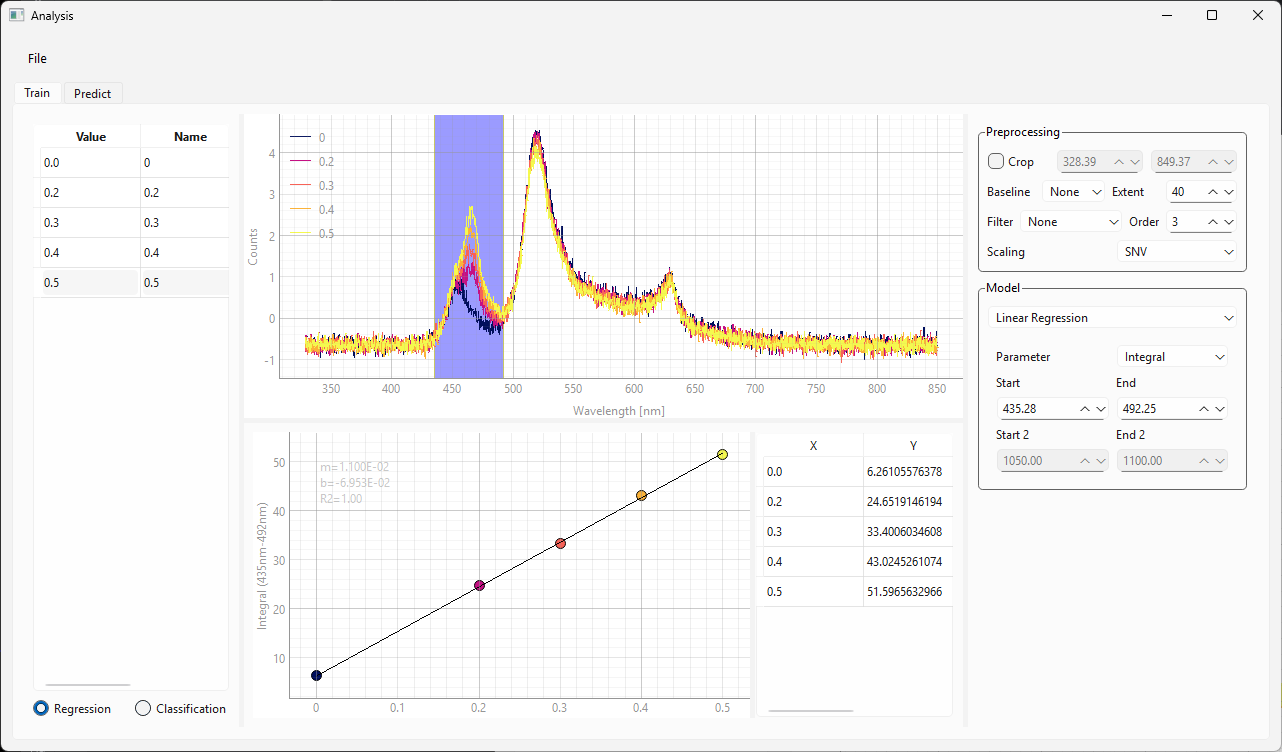
../_images/analysis_modeling_train_linearregression.png

図 3.12 モデリングウィンドウのトレーニングビュー#

回帰モデルをトレーニングするには：

  1. 分析 ‣ モデリング ‣ トレーニング/予測を使用して、モデリングウィンドウを表示します（図 3.12）。

  2. トレーニングタブを選択します（トレーニングタブは図 3.12に示されています）。

  3. 左側のサイドバーの下にあるラジオボタンセットから回帰を選択します

  4. データセットを読み込みます。これは、次のようにして実行できます。

    • スペクトルサイドバーからモデリングウィンドウの左側のサイドバーにスペクトルをドラッグする

    • 保存されたファイル（.hdf5形式）を左側のサイドバーにドラッグする

    ファイルに含まれるスペクトルがサイドバーとスペクトルビューに表示されます

  5. 各スペクトルに数値ラベルを適用します。これは、次のようにして実行できます。

    • 値列のセルをダブルクリックする

    • 数値（例：濃度）を入力する

    ヒント

    ラベリングは面倒な場合があるため、ラベル付きデータセットはファイル ‣ データセットを保存を使用して保存できます。

  6. 適切な前処理パラメーターを選択します。

    Tip

    スペクトルビューのスペクトルは、現在の前処理設定を反映します。

    図 3.12のデータでは、以下を行っています。

    • 400 nmから800 nmのスペクトル範囲を切り抜きました

    • SNVスケーリングを適用しました

    重要

    一般的に、満足のいくモデル性能を得るにはスケーリングが推奨されます。詳細については、セクション 3.4.2.1の議論を参照してください。

参考

この例では、手動の特徴選択が必要な線形回帰モデルをトレーニングしています。サポートベクター回帰モデルのトレーニングについては、セクション 3.4.3.1.2にスキップしてください。

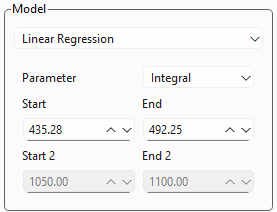
../_images/analysis_modeling_train_linearregression_settings.png

図 3.13 線形回帰設定#

  1. 図 3.13は、線形回帰分析の設定を表示します。

    • パラメーター：積分、ピーク幅、ピーク面積比など、スペクトルパラメーターの選択を可能にします。利用可能なパラメーターとその定義については、セクション 3.1を参照してください。

    • 開始と終了は、パラメーターが計算されるスペクトル範囲を決定します。このパラメーターは、スペクトルビューの領域セレクターをドラッグおよびサイズ変更することでも調整できます。

    • ピーク比率の場合、開始 2および終了 2の設定が利用可能になります

  2. 検量線（図 3.12の下部）は設定を反映します。線形トレンドラインがデータに一致するように設定を調整してください。

    • 検量線に隣接するテーブルには、曲線のX値とY値が表示されます

    • 傾き、y切片、および\(\rm{R}^2\)値は、検量線グラフに表示されます

  3. モデルに満足したら、予測タブに切り替えます（セクション 3.4.3.2）。

  4. （オプション）ファイル ‣ モデルを保存を使用して、モデルをディスクに保存します。

3.4.3.1.2. サポートベクター回帰#

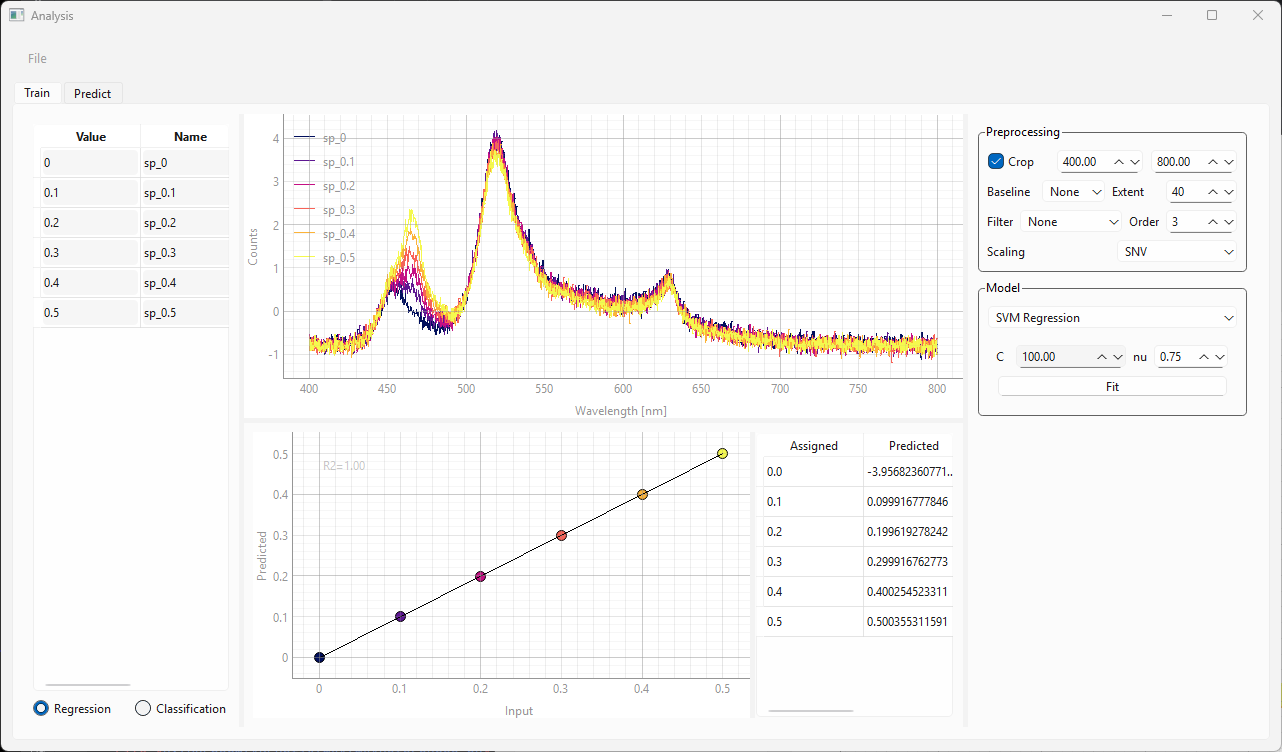
../_images/analysis_modeling_train_svr.png

図 3.14 モデリングウィンドウのトレーニングビュー（SVR）#

データの読み込み、ラベルの割り当て、および前処理は、線形回帰モデルとSVRモデルで同じです（セクション 3.4.3.1.1のステップ1-6）。

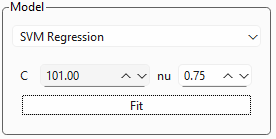
../_images/analysis_modeling_train_svr_settings.png

図 3.15 SVR設定#

図 3.15は、SVR設定ボックスの拡大図を示しており、2つのパラメーターがあります。

C

パラメーター\(C\)は、モデルの複雑さとトレーニング誤差に対する許容度の間のトレードオフを制御します。

  • 小さな\(C\)は弱いペナルティを意味します。モデルはより多くのポイントがマージンに違反することを許可し、より滑らかで単純な超平面（高いバイアス、低い分散）になります。データに多くのノイズが含まれている場合にしばしば望まれます。

  • 大きな\(C\)は強いペナルティを意味します。モデルはほとんどすべてのトレーニングポイントをマージン内に含めようと懸命になり、より複雑で曲がりくねった超平面（低いバイアス、高い分散）になります。データにノイズが含まれている場合、これは過学習につながる可能性があります。

\(\nu\)（ニュー）

\(\nu\)は、トレーニング誤差の割合（マージンの外側に落ちる外れ値）の上限と、トレーニングポイントの総数に対するサポートベクターの割合の下限を設定します。\(\nu\)は0から1の間である必要があります。\(\nu\)は、一部のSVM実装で使用される\(\epsilon\)の値を暗黙的に決定します。

  • 小さな\(\nu\)（例：0.1）：よりタイトなマージンと少ない外れ値を許可します。これは、モデルがより制限的であることを意味し、高い\(\epsilon\)に似ています。

  • 大きな\(\nu\)（例：0.9）：より広いマージンとより多くの潜在的な外れ値/サポートベクターを許可します。

フィッティング

フィッティングボタンをクリックしてモデルをトレーニングします。これにより、結果グラフと結果テーブルが更新されます。

SVRアルゴリズムは、回帰のための関連するスペクトル特徴をデータセットから自動的に抽出します。結果の曲線は、トレーニングウィンドウの下部に表示されます。この曲線は、割り当てられた（入力）数値と予測された数値を示します。理想的には、これは傾き1の直線であり、データポイントは黒い線と一致する必要があります。グラフの右側にあるテーブルには、割り当てられたラベルの数値が表示されます。

3.4.3.2. 予測#

モデルを使用するには、予測タブを選択します（図 3.16）。

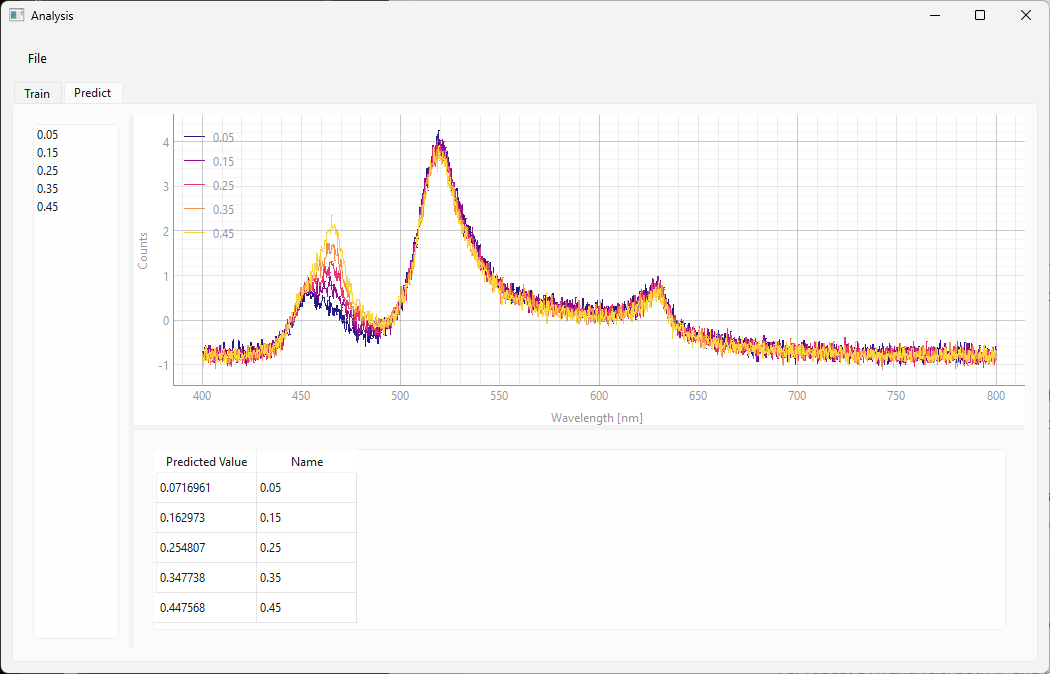
../_images/analysis_modeling_predict_svr.png

図 3.16 予測画面（SVR）#

予測タブには、トレーニングタブからの最後にトレーニングされたモデルが含まれます。または、ファイル ‣ モデルを読み込みを使用して、ディスクからモデルを読み込むこともできます。

Tip

相互検証を使用してモデルのトレーニングを最適化するために、トレーニング画面と予測画面を切り替えることができます。

モデルを使用するには：

  1. .hdf5ファイルを左側のサイドバーにドラッグしてデータを読み込みます。これにより、以下が行われます。

    • スペクトルを開く

    • モデルで選択された処理を適用する

    • 回帰分析を実行する

  2. 結果は下部のテーブルで見つけることができます。これには以下が含まれます。

    • 予測された数値

    • スペクトルの名前

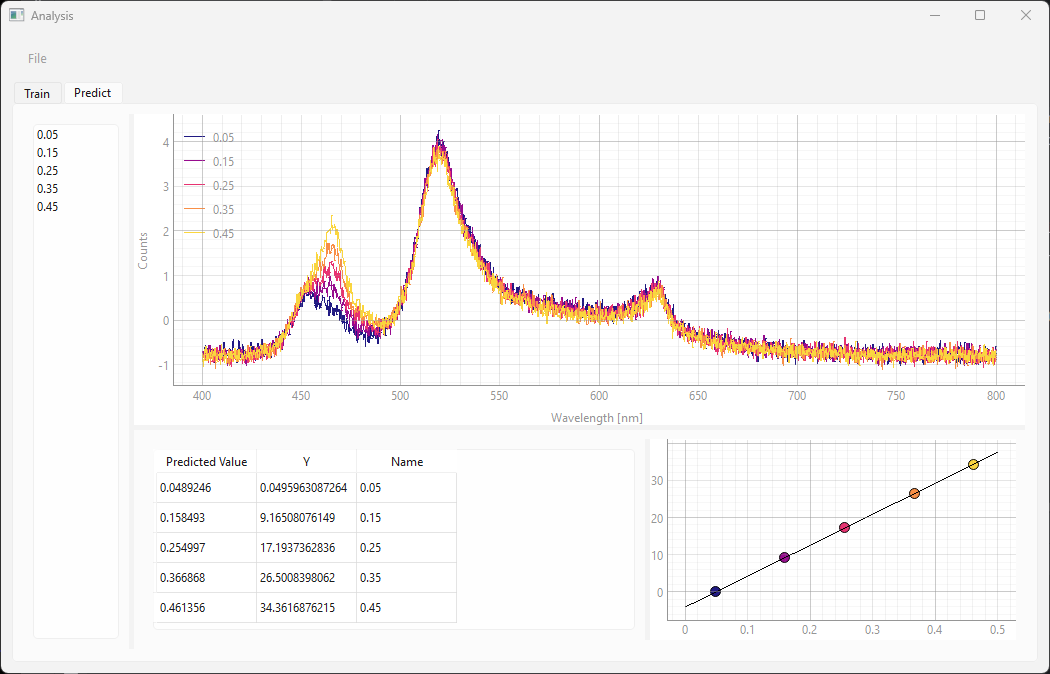
図 3.16の例では、スペクトルは既知の濃度で記録されているため、このデータセットを検証に使用できます。検証データセットの濃度は、トレーニング中に使用された濃度とは異なります。名前列には、予測されたパラメーターの（既知の）正しい値が含まれています。予測値と正しい検証値の間の一致が非常に良好であることがわかります。これは、モデルのトレーニングに成功したことを示しています。

注釈

線形回帰モデルの場合、

  • 予測画面の結果テーブルには、抽出されたスペクトルパラメーター（例：積分ピーク面積）もY列に含まれています

  • 予測画面には、検量線と、曲線上のサンプルの位置が表示されます。

例については、図 3.17を参照してください。

../_images/analysis_modeling_predict_linear.png

図 3.17 予測画面（線形回帰）#

3.4.4. 分類分析#

分類について、TII Spectrometryはサポートベクターマシン（SVM）分類を提供します。サポートベクター回帰（SVR）と同様に、SVM分類の目標は、任意のクラスの最も近いトレーニングデータポイント間のマージンが最大となる超平面を見つけることです。

参考

サポートベクター回帰に関する多くの説明は、SVM分類にも適用されます。

3.4.4.1. トレーニング#

分類モデルのトレーニングは、一般的にセクション 3.4.3.1.1で示されている手順を反映しています。

  1. 分析 ‣ モデリング ‣ トレーニング/予測を使用して、モデリングウィンドウを表示します（図 3.18）。

  2. トレーニングタブを選択します（トレーニングタブは図 3.18に示されています）。

  3. 左側のサイドバーの下にあるラジオボタンセットから分類を選択します

  4. データセットを読み込みます。

  5. データセットにラベルを適用します。ラベルは任意のテキストにすることができます。

    Tip

    ラベル付きデータセットはディスクに保存できます

  6. SVMのハイパーパラメーター\(C\)と\(\nu\)（セクション 3.4.3.1.2）を調整し、フィッティングをクリックしてモデルをトレーニングします。

  7. 下部の結果ビューには、混同行列が表示されます。これは、予測されたラベルと割り当てられたラベルをプロットしたものです。理想的には、すべての値が対角線上に位置します。

  8. モデルに満足したら、予測タブに切り替えます。

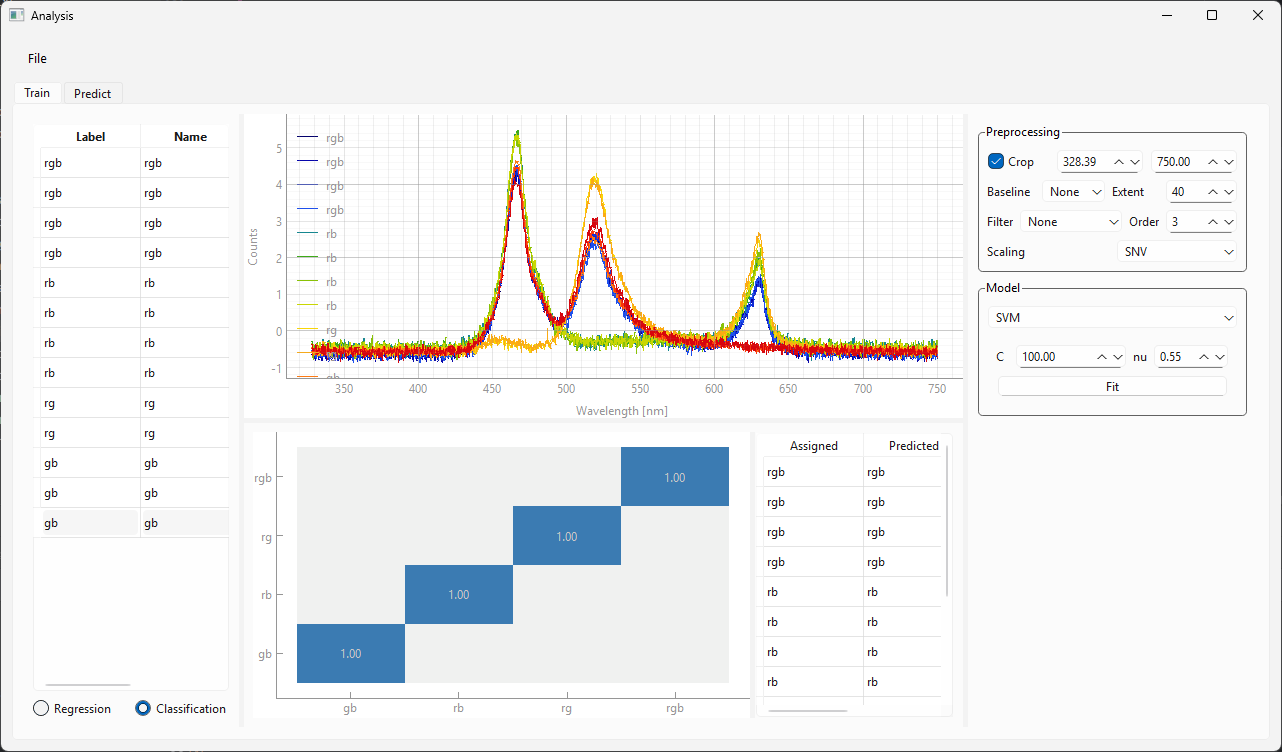
../_images/analysis_modeling_train_svm.png

図 3.18 分類モデルのトレーニング。#

3.4.4.2. 予測#

トレーニングされた分類モデルを予測に使用する方法は、回帰モデルの使用方法を反映しています。

手順はシンプルです。

  1. .hdf5ファイルを左側のサイドバーにドロップしてデータセットを読み込みます。

  2. 分類結果は下部のテーブルに表示されます（図 3.19）。

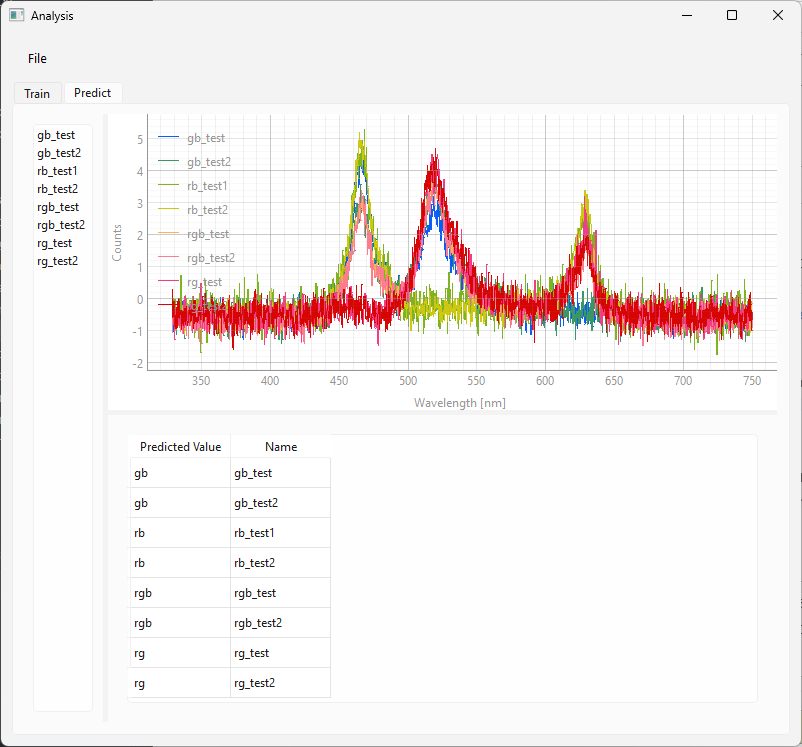
../_images/analysis_modeling_predict_svm.png

図 3.19 分類モデルの使用。#

図 3.19のデータセットでは、予測に使用されたスペクトルの名前の最初の部分に正しいラベルが含まれています。予測値と正しいラベルの一致が優れていることがわかります。

3.4.5. モニタリング#

トレーニングされたモデル（分類モデルと回帰モデルの両方）をTII Spectrometryでリアルタイムモニタリングに使用できます。例：

  • 回帰モデルを使用して濃度をモニターする場合

  • 異なる物質を識別する場合

この機能には、分析 ‣ モデリング ‣ モニターを使用してアクセスし、モニタリング画面（図 3.20）を表示します。ここでは、

  • 読み込みボタンを使用してモデルを読み込むことができます

分光器を単一または連続取得モードで使用している場合、現在取得されているスペクトルに対する選択されたモデルの予測結果が右上に表示されます。

重要

予測結果は表示されるだけで、ディスクには保存されません。予測結果を記録するには、タイムラプス取得を使用してください。

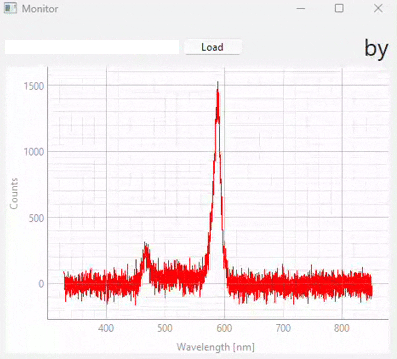
../_images/analysis_model_monitor_RT1.png
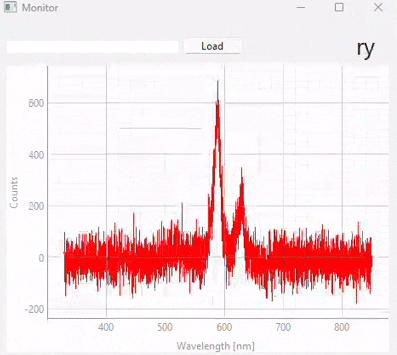
../_images/analysis_model_monitor_RT2.png
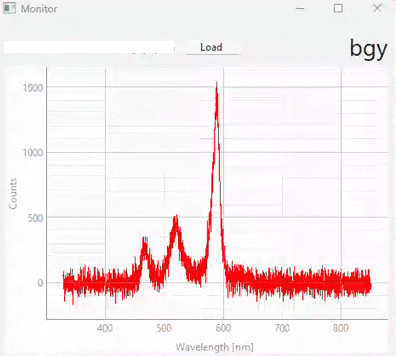
../_images/analysis_model_monitor_RT3.png
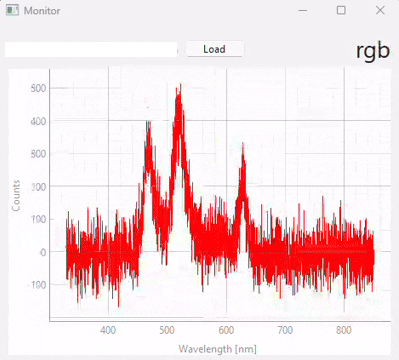
../_images/analysis_model_monitor_RT4.png
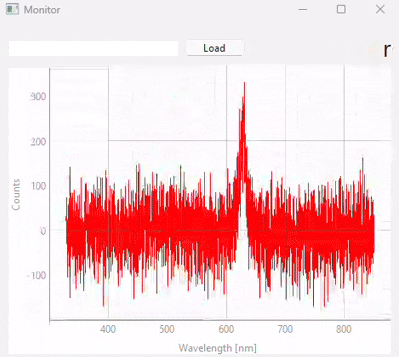
../_images/analysis_model_monitor_RT5.png
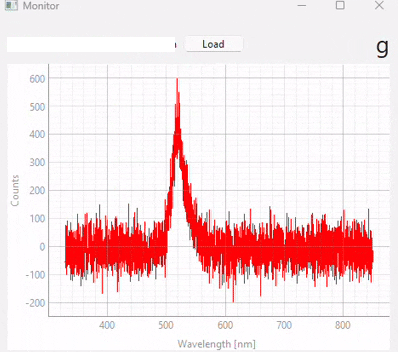
../_images/analysis_model_monitor_RT6.png

図 3.20 Real-time monitoring (snapshots)#

図 3.20は、異なる時点での予測結果のスナップショットを表示しています。この実験で使用されたデータセット/モデル（多くの異なるサンプルクラスが含まれています）は、図 3.21に表示されています。以下の点に注意することが重要です。

  • テストスペクトル（モニタリング中）のS/N比は、トレーニングに使用されたスペクトルのS/N比よりも大幅に低くなっています。適切なスケーリングと比較的ノイズ耐性のあるSVMモデルのおかげで、これは予測段階で悪影響を及ぼしません。

  • 予測の忠実度は優れており、誤分類はありません

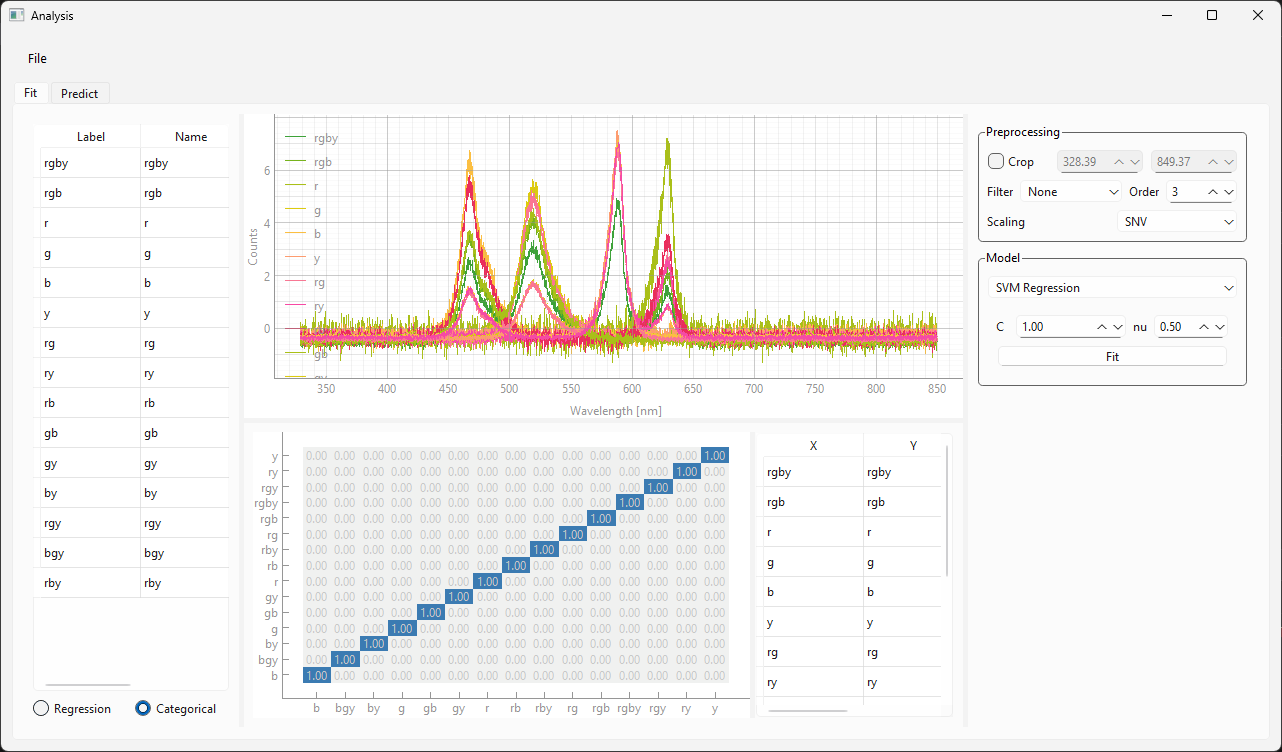
../_images/analysis_modeling_monitoring_model.png

図 3.21 モニタリング実験に使用された分類モデル。#

目次