FTIRデータに適用される高速フーリエ変換（FFT）

5.1. FTIRデータに適用される高速フーリエ変換（FFT）#

この節では、主に教育目的として、フーリエ変換赤外分光計からの空間または時間領域インターフェログラムデータからスペクトルを抽出する方法について説明します。

図 5.1（左）は、両側インターフェログラムを示しています。x 軸は、光路差（OPD）—干渉計のミラーが移動した距離をメートル単位で示しています。右パネルは、機器によって最大干渉が生成されるゼロOPD領域付近のバーストを示しています。

注釈

これは、ARCoptix FTIR機器によって提供されるデータです。

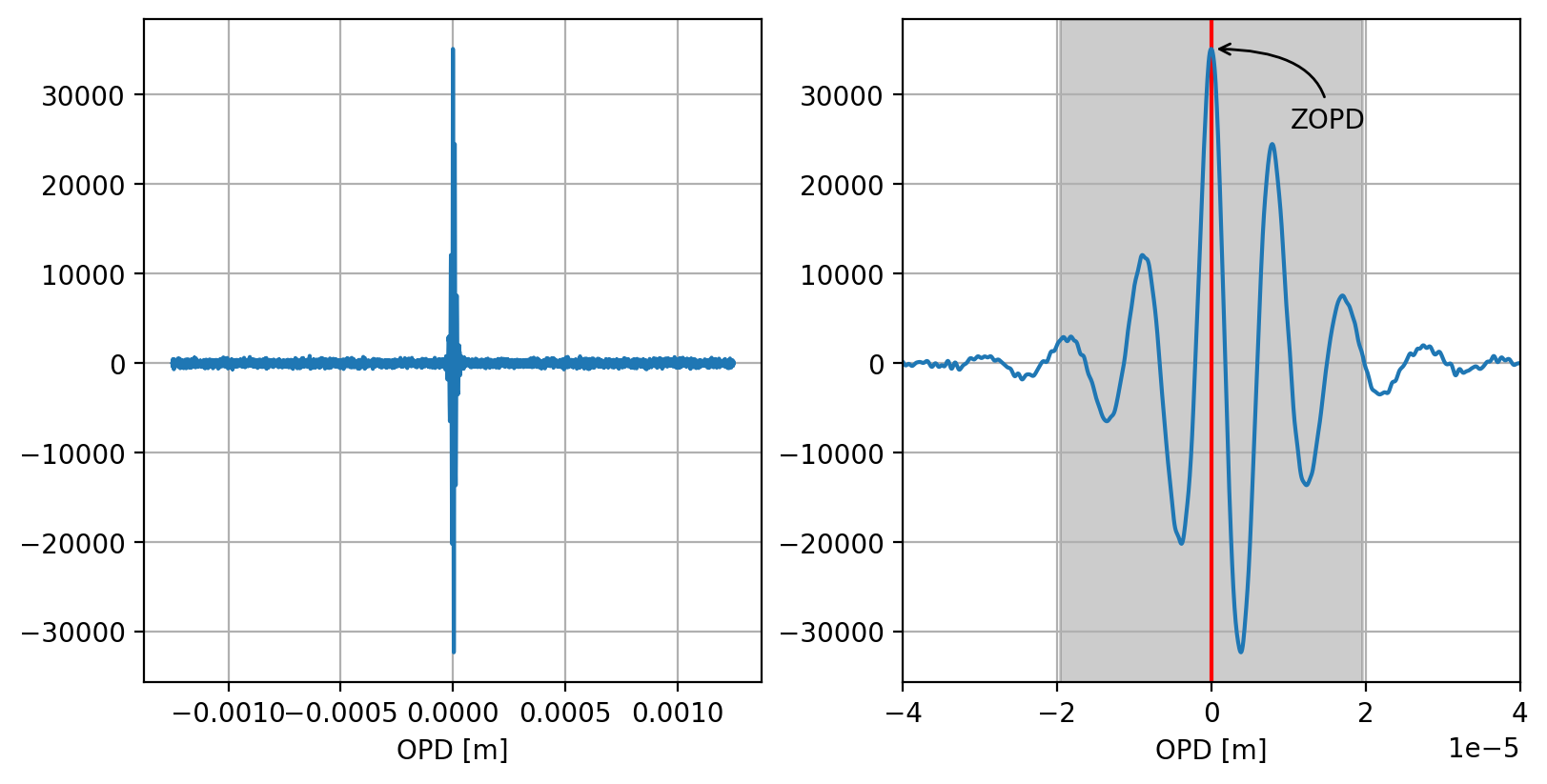
../_images/appendices_FFT_data.png

図 5.1 インターフェログラム（左）とZOPD領域の拡大図（右）#

このデータからスペクトル情報を抽出するには、次の手順が必要です。

  1. （オプション）インターフェログラムのパディング。空間領域でのパディングは、波数領域での補間と同等であり、スペクトル分解能を向上させるために実行できます。

  2. 位相補正データの準備

  3. 位相補正されたインターフェログラムからのサンプルスペクトルの抽出

  4. （オプション）参照スペクトルを使用した吸収または透過スペクトルの計算

スペクトル \(B(\nu)\) は、インターフェログラム \(I(\Delta)\) の複素フーリエ変換を行うことによって得られます。

\[B(\nu) = \int_{-\infty}^{+\infty} I(\Delta) e^{-i 2 \pi \nu \Delta} d\Delta\]

ここで：

  • \(I(\Delta)\) は、光路差（\(\Delta\)）の関数としてのインターフェログラムです。

  • \(\nu\) は波数です。

5.1.1. 位相補正#

理想的なフーリエ変換（FT）システムでは、インターフェログラム（検出器によって収集された生信号）は、干渉計内の2つの光路が完全に等しくなるゼロ光路差（ZOPD）点を中心として完全に対称である必要があります。しかし、実際のFTIR機器では、主に以下のいくつかの要因により、位相誤差（\(\theta(\nu)\)）が発生します。

  • 機器の不完全性：光学部品（ビームスプリッター材料など）は波長依存の屈折率（分散）を持つため、異なる波長が材料内をわずかに異なる速度で通過します。

  • サンプリング/エレクトロニクス：ZPDと記録された最初のデータポイントとの間のわずかなオフセット、または電子フィルター効果。

ここで使用される位相補正方法は、周波数（波数）領域で機能する乗法補正方法である Mertz 法です。これは位相誤差を推定し、測定された全スペクトルからそれを取り除きます。

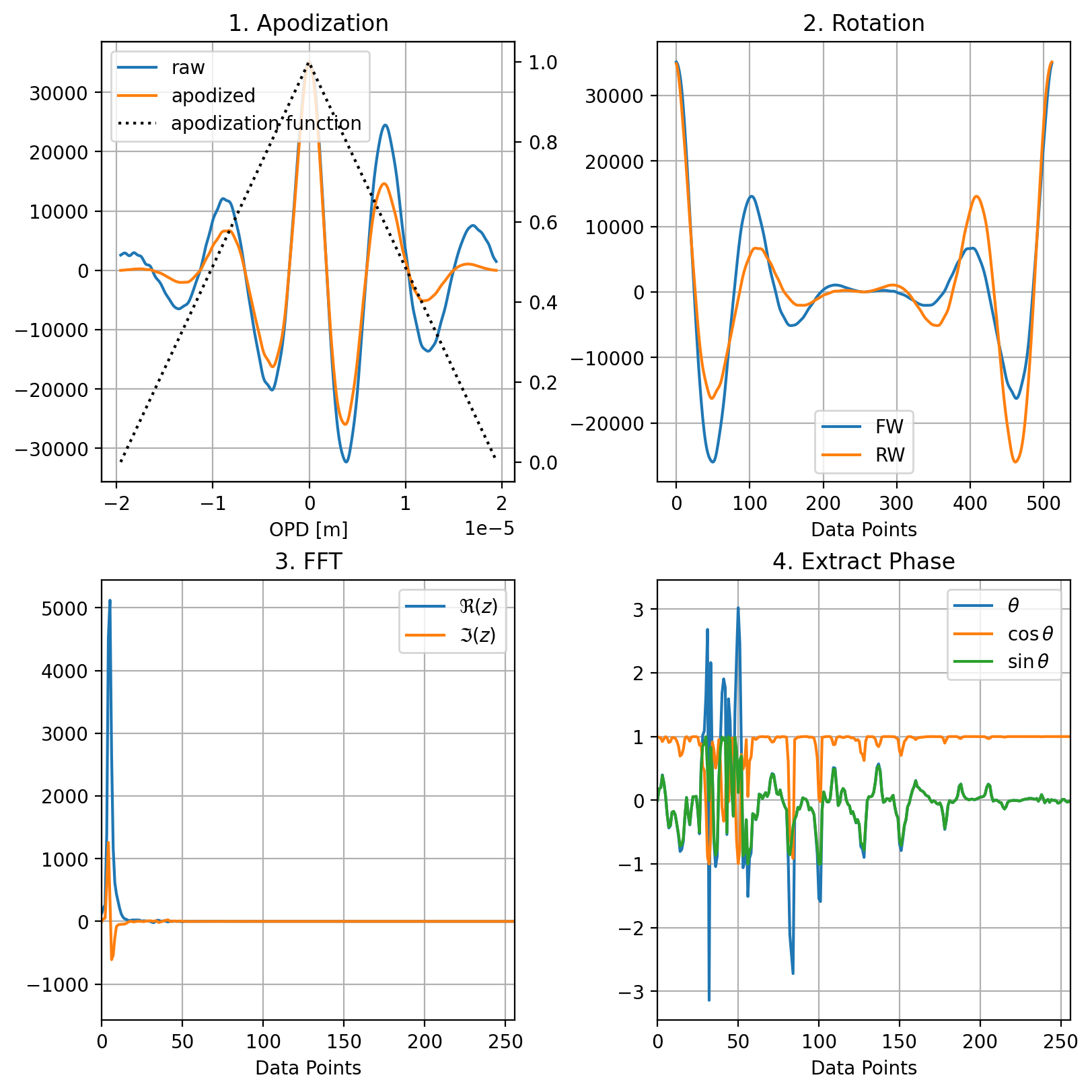
../_images/appendices_FFT_phase.png

図 5.2 位相補正#

この方法は、機器の位相 \(\theta(\nu)\) が波数の緩やかな関数であるという仮定に基づいています。これにより、S/N比が最も高いセンターバースト（ZOPD）周辺のインターフェログラムの小さな、高度に対称な領域（図 5.1の灰色で陰影を付けられた領域）から位相を正確に決定することができます。

  • ZOPDを中心とした小さな領域（図 5.2) \(I_{short}(\Delta)\) を抽出します

  • エッジ効果を避けるためにこの領域をアポダイゼーションします。ここでは、三角形関数を使用して \(I'_{short}(\Delta)\) を得ます

  • ZOPDデータを0にシフトするようにデータを回転させます

  • フーリエ変換（FFT）を実行します

  • 結果として得られる複素スペクトルは、実部と虚部の関係を使用して、位相スペクトル \(\theta(\nu)\) を計算するために使用されます。

    \[ \theta(\nu) = \arctan \left( \frac{\Im(z)}{\Re(z)} \right) \]

    ここで \(z\) は \(I'_{short}(\Delta)\) の複素フーリエ変換です

5.1.2. サンプルスペクトルの抽出#

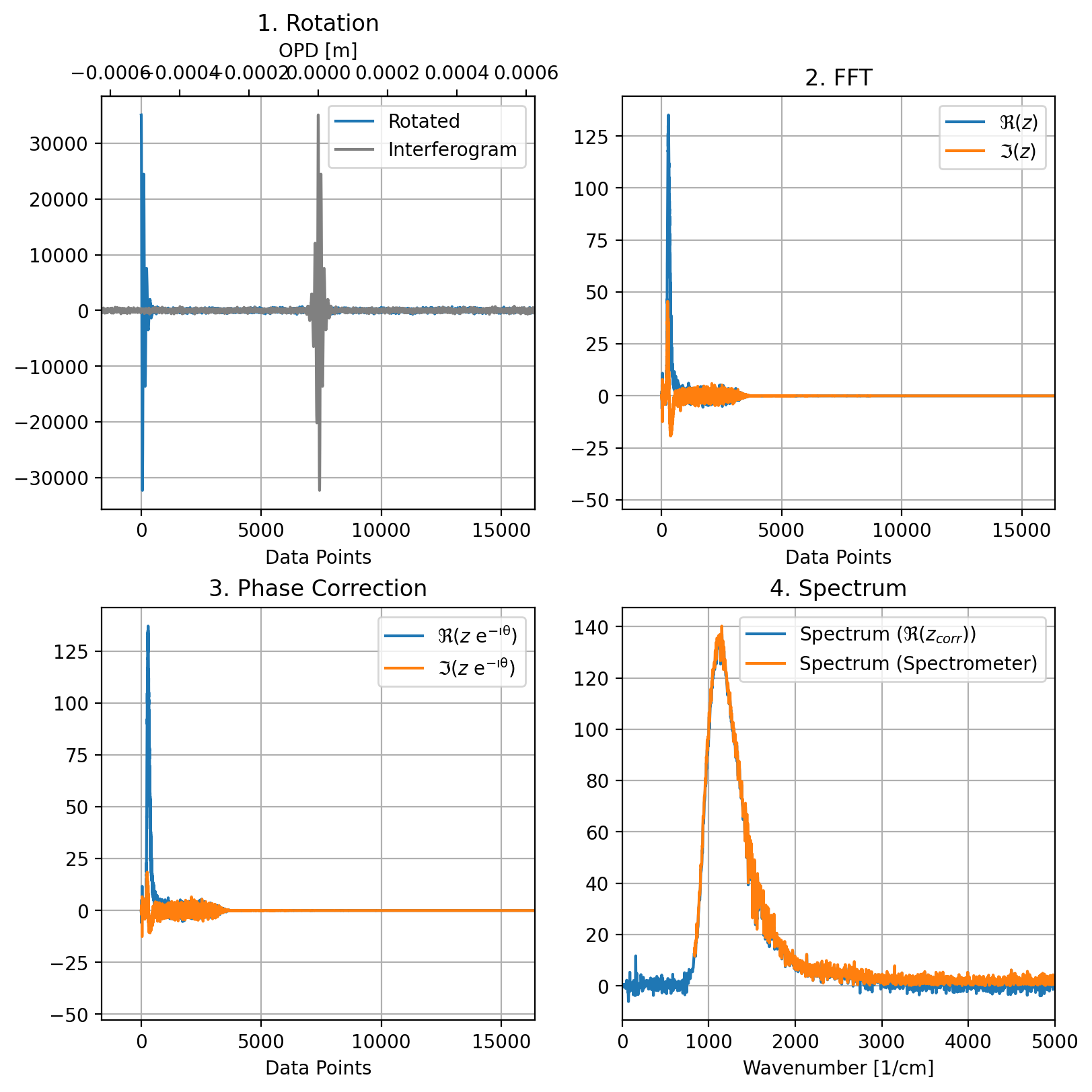
../_images/appendices_FFT_sample.png

図 5.3 スペクトルの抽出#

位相 \(\theta(\nu)\) が得られたら、全スペクトルの位相補正を行うことができます。この目的のために：

  • 位相スペクトル \(\theta(\nu)\) は、最終的に必要なスペクトルの完全な分解能に補間されます。

  • 全インターフェログラムを回転させて、ZOPDデータをビン0にシフトします

  • 回転されたデータにFFTが適用されます

  • 完全な片側インターフェログラムの複素フーリエ変換に補正項を乗算することにより、最終的な位相補正が適用されます。

    \[ B_{corrected}(\nu) = B_{full}(\nu) \cdot e^{-i \theta(\nu)}\]

  • スペクトルは、\(B_{corrected}(\nu)\) の実部 \(\Re(B_{corrected}(\nu))\) となります

図 5.3 パネル4は、この方法（青）で抽出されたスペクトルと分光計によって取得されたスペクトル（オレンジ）を比較しています。全体的な形状は似ていますが、強度が異なります。これは、分光計がスペクトル分解能を向上させるためにゼロパディングを2倍の係数で使用しているためです。FFTは \(\rm{1/n}\) でスケーリングされるため、これは振幅にも影響します。

5.1.3. 結果#

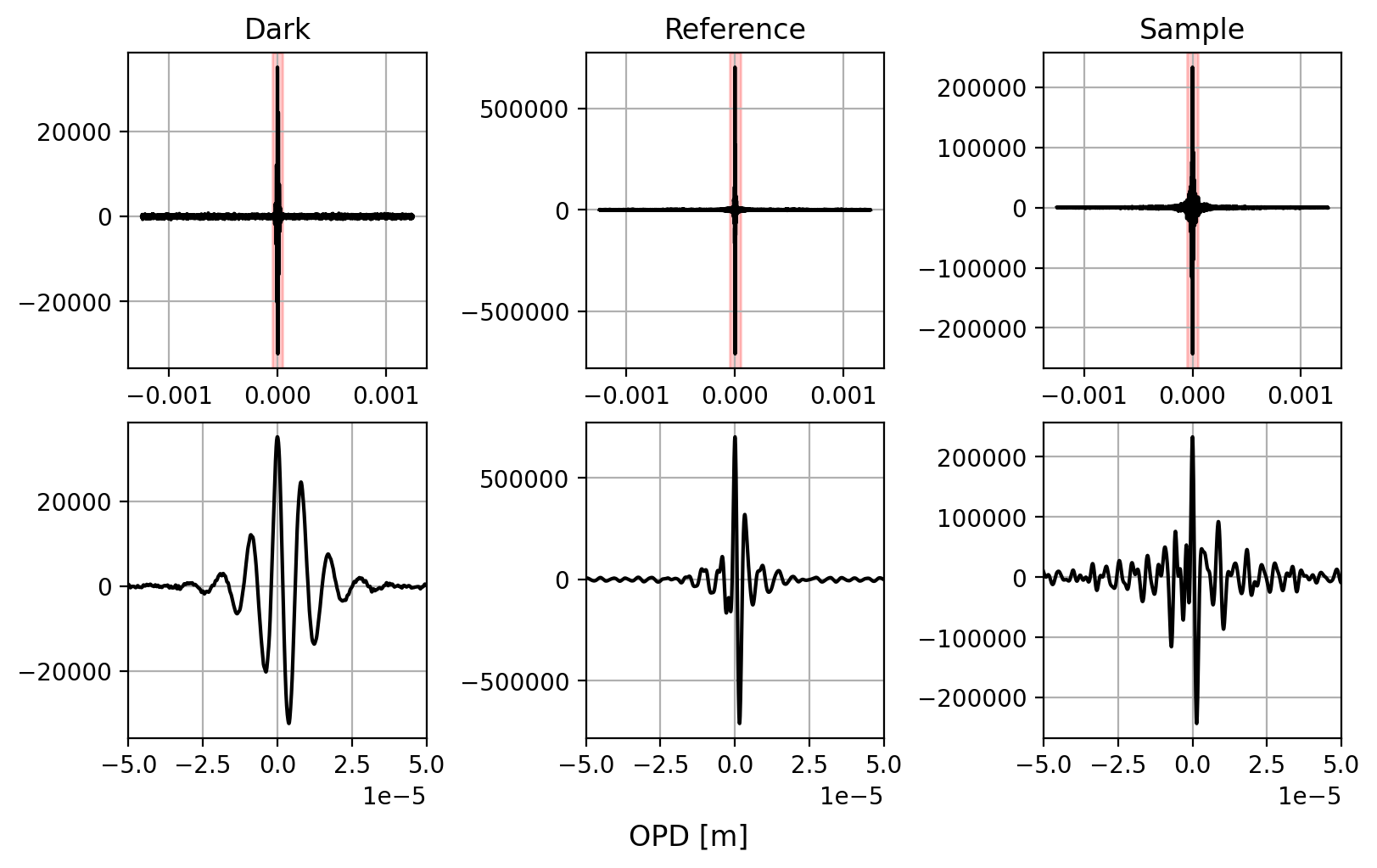
../_images/appendices_FFT_comparisons_interferogram.png

図 5.4 干渉図の例#

図5.5は、干渉計画像（図5.4）から手動で抽出したスペクトルと分光計のデータ処理結果を比較したものである。3つのスペクトルを示す：

  • 光が検出器に当たらないダークスペクトル

  • 空気の参照スペクトル

  • かなり厚いポリスチレンサンプルのサンプルスペクトル

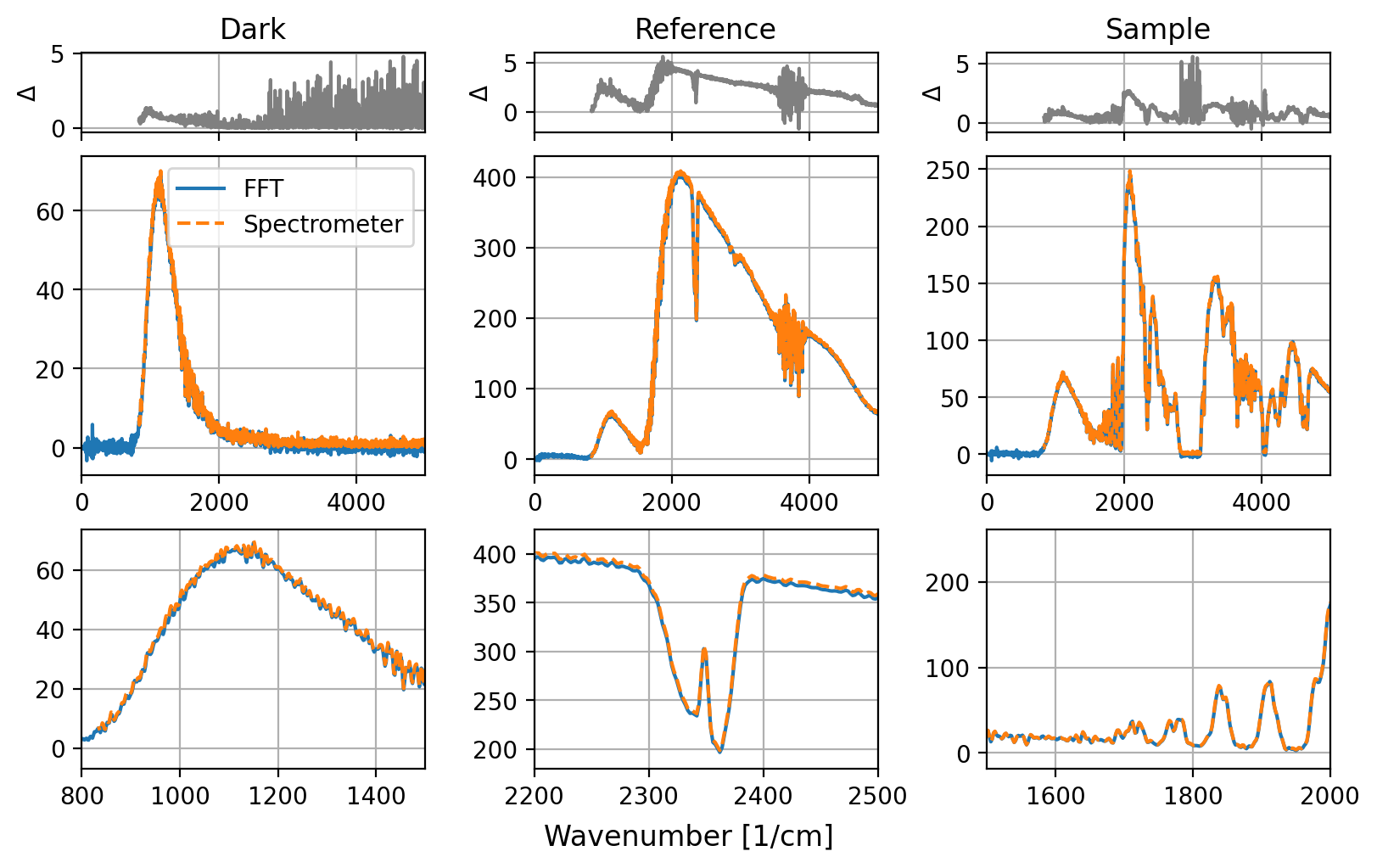
../_images/appendices_FFT_comparison1.png

図 5.5 インターフェログラム分析#

分析のために：

  • データは2の係数でゼロパディングされました

  • 位相補正データは 節 5.1.1 で示されているように準備されました

  • 全インターフェログラムはフーリエ変換され、位相補正され、スペクトルは実部から計算されました。

全体として、手動処理と分光計の結果との間の一致は非常に良好です。残差（2つの方法で得られたスペクトルの差、図 5.5の最上行）は通常非常に小さく、総信号強度のわずか数パーセントにすぎません。より大きな差は、カウント率が非常に低い領域、例えば波数3000 cm-1を超えるダークスペクトルや、2800〜3200 cm-1のポリスチレンサンプルで発生します。

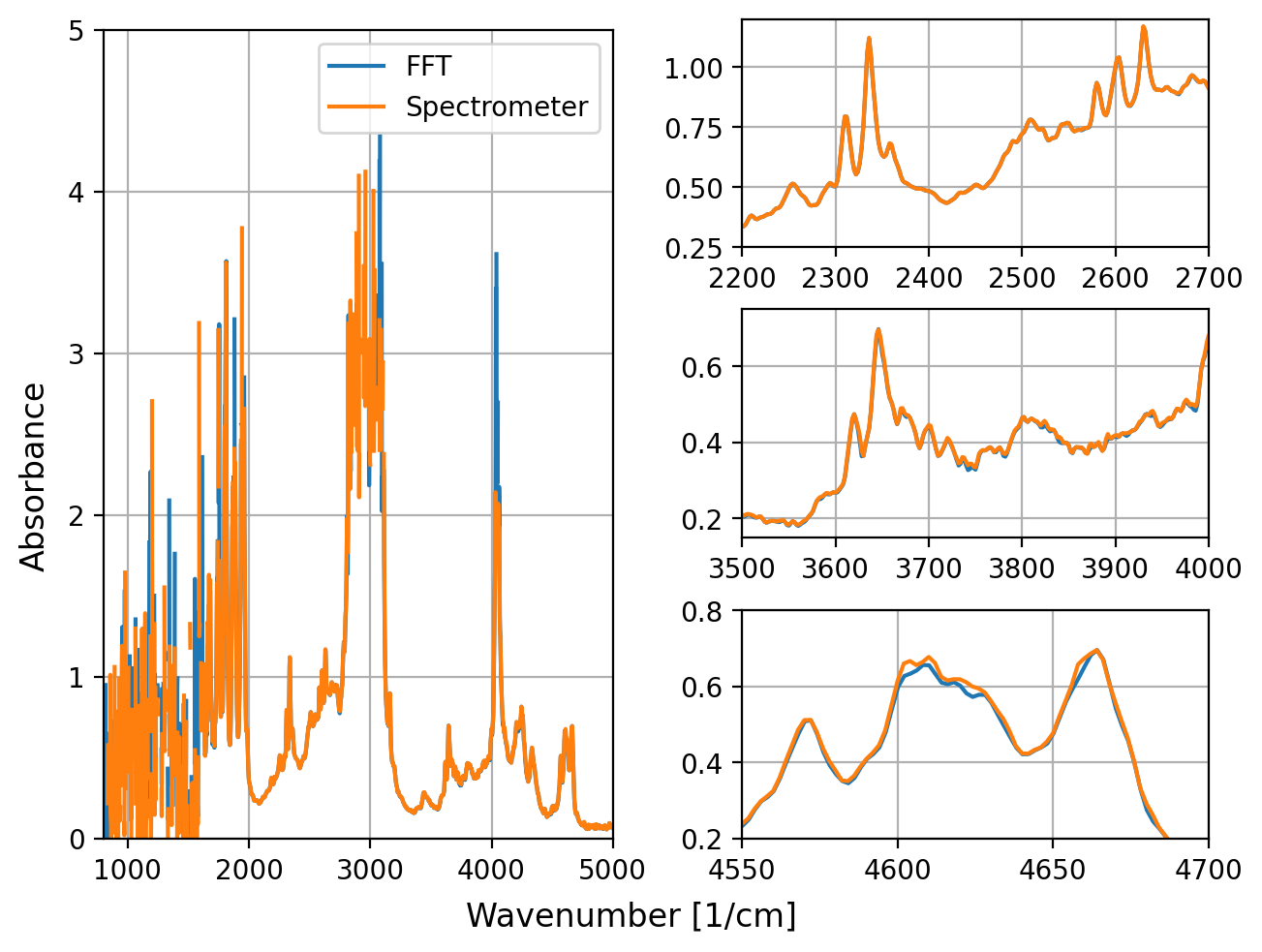
../_images/appendices_FFT_absorbance.png

図 5.6 吸光度スペクトル#

図 5.6 は、生データから計算された吸光度スペクトル \(\rm{A(\nu)}\) を示しています

\[ A(\nu) = -\log_{10}{\frac{I_S(\nu) - I_B(\nu)}{I_R(\nu) - I_B(\nu)}} \]

ここで：

  • \(\rm{I_S(\nu)}\) はサンプルスペクトルです

  • \(\rm{I_R(\nu)}\) は参照スペクトルです

  • \(\rm{I_B(\nu)}\) はバックグラウンド（ダークカウント）スペクトルです

ここでも、高い吸光度の領域を除いて一致は非常に良好です。これらの領域では、除算と対数の適用により、わずかな数値の違いでさえ強調されます。図 5.6 の右パネルは、主要なスペクトル領域の比較を示しており、一般的に一致は優れています。

5.1.4. 注釈付きの例#

この節には、インターフェログラム分析を実行するためのPythonサンプルコードが含まれています。numpy が利用可能であることを前提としています。

5.1.4.1. CSVデータの読み込み#

このスニペットは、.csv データを opd および y numpy 配列に読み込みます。

1data_sp = np.loadtxt("data.csv", skiprows=1, delimiter=',')
2opd, y =  data_sp[:, 0], data_sp[:, 1]

5.1.4.2. パディング#

ここでは、（オプションで）データを fillFactor でパディングします。これはスキャン範囲を増やすことと同等であるため、opd 配列は現在、2倍の範囲を持つ2倍の数のポイントの配列になります。y 強度データは、開始と終了にゼロを付加することによって対称的にパディングされます。

1opd = opd * fillFactor
2opd = np.linspace(opd.min(), opd.max(), len(opd) * fillFactor)
3y = np.pad(y, pad_width=(int((fillFactor - 1) / 2 * len(y)),), mode='constant')

5.1.4.3. 位相抽出#

まず、ZOPDのインデックスを取得します。

次に、

  • 512ポイントのウィンドウを使用して、ZOPDの周りの小さな領域 yShort を抽出します

  • 三角形アポダイゼーションを使用して y_apo を準備します

  • np.roll を使用してZOPDビンを0に回転します

  • np.fft を使用してFFTを計算し、atan2 関数を使用して位相 theta を計算します

 1max_Y = np.argmin(np.abs(opd))
 2
 3winSize = 512
 4xShort = np.arange(0, winSize)
 5yShort = y[max_Y - winSize//2 :max_Y + winSize//2]
 6
 7apo_short = triangularApodization(yShort)
 8y_apo = yShort * apo_short
 9y_short_apo_rot = np.roll(y_apo[::1], winSize//2)
10fft_short = np.fft.fft(y_short_apo_rot, norm='forward')
11theta = np.atan2(fft_short.imag, fft_short.real)

5.1.4.4. スペクトルの計算#

まず、（パディングされた）スペクトルの全長に位相情報を補間します。

1theta_full = np.interp(np.linspace(xShort[0], xShort[-1], len(opd)), xShort, theta)

次に、スペクトルを計算します。

  • np.roll を使用して回転します

  • FFTを実行します

  • FFTの実部に \(\exp(- i\theta(\nu))\) を乗算することで、位相補正を適用します

  • スペクトル yy を、位相補正された成分の実部として計算します。

  • （位相補正後）スペクトルが対称になるため、OPDの半分の長さにこれを切り詰めます

1#alternatively, apply apodization here, eg
2#y_apo = y * triangularApodization(y)
3y_apo = y 
4y_full_apo_rot = np.roll(y_apo[::1], -max_Y)
5fft_full = np.fft.fft(y_full_apo_rot, norm='forward')
6
7yy = (fft_full * np.exp(-complex(0,1)*theta_full)).real[0:len(xx)]

5.1.4.5. 波数軸の計算#

最後に、波数軸を計算する必要があります。まず、波数増分 dx を cm-1 で計算し、dx をステップサイズとして使用して numpy 配列 xx を埋めます。

1dx = 1/(opd.max() + np.abs(opd.min())) / 100 
2xx = np.linspace(0, len(opd)//2 * dx, len(opd)//2)

5.1.4.6. アポダイゼーション#

データ y の三角形アポダイゼーション関数は、以下の関数を使用して計算できます

1def triangularApodization(y:np.ndarray):
2    max_Y = np.argmax(y)
3    x = np.arange(0, len(y))
4    apo = 1-np.abs(x - max_Y) / (1 * len(x[max_Y:])) 
5    apo[apo < 0] = 0
6    return apo

あるいは、

  • Norton-Beer パッケージには、FTIR分析で一般的に使用される関数が多数含まれています

  • 標準的な窓関数（ハニングなど）も同様に機能します。

目次